|
|
|
|
|
|
|
|

| Disclaimer Information in this document is provided in connection with Intel products. No license, express or implied, by estoppel or otherwise, to any intellectual property rights is granted by this document. Except as provided in Intel's Terms and Conditions of Sale for such products, Intel assumes no liability whatsoever, and Intel disclaims any express or implied warranty, relating to sale and/or use of Intel products including liability or warranties relating to fitness for a particular purpose, merchantability, or infringement of any patent, copyright or other intellectual property right. Intel products are not intended for use in medical, life saving, or life sustaining applications. Intel may make changes to specifications and product descriptions at any time, without notice. Copyright © Intel Corporation (1996). Third-party brands and names are the property of their respective owners.
|
|
1.0. INTRODUCTION
3.0. MMX TECHNOLOGY BASEBAND ECHO CANCELER IMPLEMENTATION |
The media extension to the Intel Architecture (IA) instruction set includes single instruction, multi-data (SIMD) instructions. This application note presents an implementation of a common modem algorithm that takes advantage of these new instructions. Specifically, the baseband echo canceler function, ecmmx, demonstrates how the PMADDWD instruction can be used to perform complex FIR calculations efficiently and how use of the PUNPCKL and PUNPCKH instructions allow the adaptation of several filter coefficients at a time within a single loop.
The are two sources of echo in a modem. The near end (NE) echo signal is a combination of the reflection of the transmitted signal due to the impedance mismatches of the lines at the hybrid transformer on the modem board and the mismatches at the Public Switch Telephone Network(PSTN). The far end echo signal is a combination of the reflection of the transmitted signal due to impedance mismatches of the lines at the far end hybrid transformer on the receiving modem board and the mismatches at the far end of the PSTN (Figure 1). The near end echo has a much larger amplitude than the far end echo. The algorithm is the same for both the near end and far end echo cancelers. The difference is in the amount of delay in the buffer that holds the transmitted data used in the filter calculation, the delay is longer for the far end.
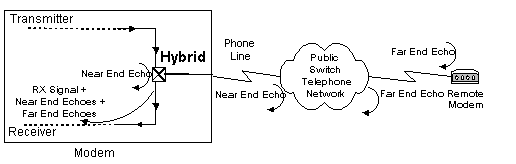
The baseband echo canceler is an adaptive filter that effectively cancels out the near and far end echos allowing the transmitted signal from the remote modem to arrive more cleanly at the receiver. The echo canceler can adapt because it knows the characteristics of its transmitted signal which appears in the echoes and can therefore subtract it out from the combined signal made up of the received signal and the echoes.
The MMX technology version of the baseband echo canceler consists of four parts:
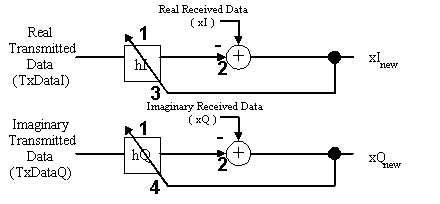
Figure 2 shows the core operation performed by the code presented in this paper. The code loops three times to process each received baud that arrives at the modem because each baud is represented by three complex samples stored in the xI and xQ arrays. As a result, there are three pairs of complex filters that need to be calculated in the MMX technology version of the baseband echo canceler.
The data and received signal arrays, txdataI, txdataQ, xI, and xQ, are all 16-bit signed fixed point fractions. The coefficients, hI and hQ, are represented as 32-bit signed fixed point fractions but are stored as two 16-bit value arrays, hIH and hIL for the real coefficients and hQH and hQL for the imaginary coefficients. This is done because the higher 16 bits of the coefficients are used in the filter calculation while all 32 bits are used in the adaptation of the coefficients. These coefficients start out initialized as 0. The 'I' notation on the array names indicates the real part of the complex value and the ' Q' notation indicates the imaginary part. The hI arrays are stored in memory as [hIH0 hIH1 hIH2] and [hIL0 hIL1 hIL2] where each of the subscripts denotes one of the three complex filters while the hQ arrays are stored as [hQH0 hQH1 hQH2] and [hQL0 hQL1 hQL2]. Each filter is the same length which must be a multiple of 8 in this implementation.
The formula used to calculate the complex FIR output is as follows:
where txdata is the transmitted data and h are the filter coefficients
The formula for the calculation of the real output and imaginary output were derived as follows:
real filter output:
imaginary filter output:
By using the PMADDWD instruction the filter loop can be performed quite efficiently. In each loop iteration it is possible to calculate two of the multiply/add and subtract operations for the real filter output calculation and two multiply and add operations for the imaginary filter output calculations. Only the high order 16-bits of the coefficients are used in this calculation. The following figure shows how the filter is performed. Register MM0 is used as the accumulator for the real filter output while MM1 is used for the imaginary filter output.
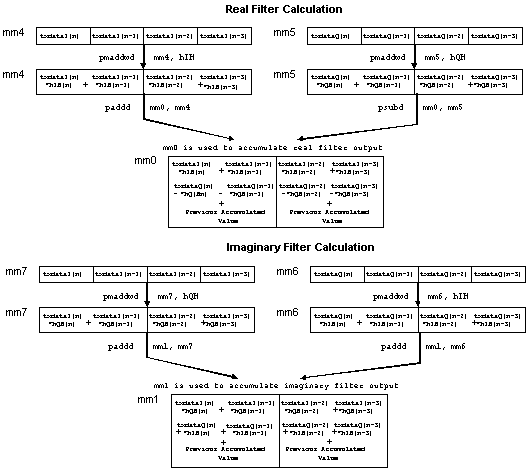
There are a few initial conditions set before the complex FIR loop is entered. Register MM4 is preloaded with the first four values in the txdataI array and the accumulator registers are cleared. These instructions are done so that the loop of the FIR filter can be paired efficiently. As a result of this instruction reordering, after the loop is complete MM5 and MM6 must be subtracted from MM0 and added to MM1 respectively.
; Complex FIR Loop FIRLoop: pmaddwd mm4, [ecx+edi] ; Compute txdataI*hIH value psubd mm0, mm5 ; Accumulate real filter sum movq mm5, [ebx+edi] ; Read in txdataQ values paddd mm1, mm6 ; Accumulate imag. filter sum pmaddwd mm7, [edx+edi] ; Compute txdataI*hQH value movq mm6, mm5 ; Copy txdataQ value from mm5 pmaddwd mm5, [edx+edi] ; Compute txdataQ*hQH value paddd mm0, mm4 ; Accumulate real filter sum movq mm4, [eax+edi+8] Load next set of txdataI to be used pmaddwd mm6, [ecx+edi] ; Compute txdataQ*hIH value paddd mm1, mm7 ; Accumulate imag. filter sum movq mm7, mm4 ; Copy txdataI value from mm4 add edi, 8 ; Increase data pointer by 8 bytes sub esi, 4 ; Decrement counter value jg FIRLoop ; If no more filter taps then done with ; loop ;End of Loop for FIR psubd mm0, mm5 ; Final accumulate for real filter paddd mm1, mm6 ; Final accumulate for imag filter)
To get the final result of the real filter MM0 is then copied into MM2 and shifted right by 32 bits and added back to MM0. The imaginary result mm1 is copied to MM3 and shifted right by 32 bits and added back to MM1. These values are then scaled to 16-bit values so the new received signal can be calculated.
The values of the received data, both real and imaginary are then read into a register and the filtered echo signal is subtracted from them.
xInew = xIreceived yI where yI is the real filtered value
These new xI and xQ are stored back into memory and are also used as the error signal used to adapt the coefficients of the filters (see Figure 2).
The are two loops that take care of the filter coefficient adaptation. First, the real coefficients are adapted and then the imaginary coefficients are calculated in the second loop. This is done because the technique used did not leave enough MMX registers to accomplish both adaptations within one loop. The error signals were stored in the way they were(see figure 4) so that for every loop iteration four coefficients could be adapted at a time. The following equations were used for adaptation:
where m = adaptation step size (0.125 in this code), e = error signal (xInew and xQnew in this code), and d* = the conjugate of the transmitted data (txdata in this code).
Expanding out the above equation provides the individual equations used in the adaptation loops.
In the above equations notice that for the adaptation of the filter coefficients the error values, xInew and xQnew, must be multiplied by each data value, txdataI or txdataQ, associated with the coefficient being adapted. For example, to adapt the first coefficient hI[0](full 32-bit value) the error value xInew would be multiplied with txdataI[0] and value xQnew would be multiplied with txdataQ[0] and they would be added together. By storing the complex error signals interleaved with zeroes, multiple adaptation of coefficients can occur in the adaptation loops.
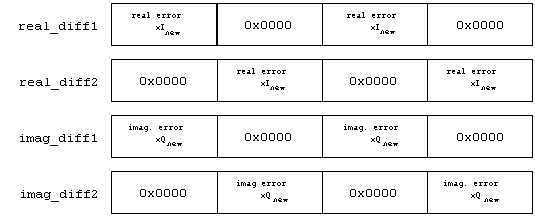
For example, by using real_diff1, the PMADDWD instruction, and the txdataI value and adding it to the result of using imag_diff1, the PMADDWD instruction, and the txdataQ value to the second and fourth coefficients could be adapted (see Figure 5). After the PADDD instruction is performed the data then only needs to be shifted by three bits to the right, which equates to a multiplication of m equal to 0.125, and it is ready to be added to the previous 32-bit coefficient for adaptation(see Figure 6). Similiarly, real_diff2 and imag_diff2 are used to calculate the adaptation for the first and third coefficient. The adaptation equation is described in further detail in the next section.
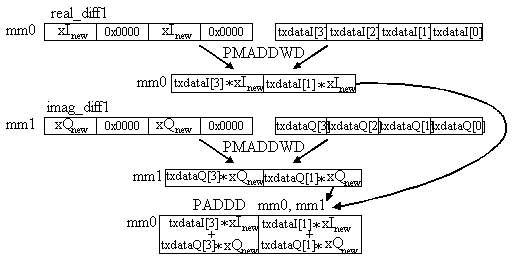
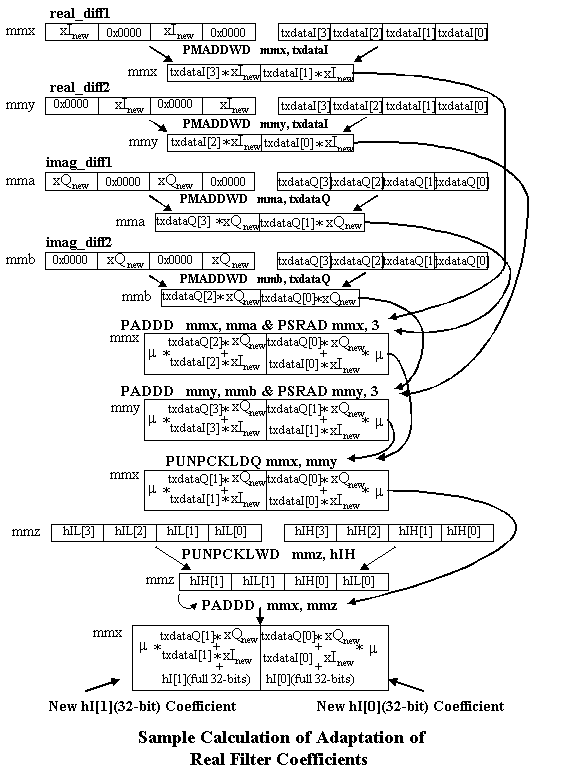
Figure 6 shows in more detail how the adaptation of the first two real coefficients is done. These same instructions are used in the adaptation loops to accomplish the adaption of the next six real coefficients. The same instructions are used in the adaptation of the imaginary coefficients.
Since the coefficients are 32-bits but are stored in an array of high 16-bit coefficients and an array of low 16-bit coefficients, unpacking and shifting operations must be used to manipulate the data properly to get the correct outcome of the equation for filter coefficient adaptation. The PUNPCKHWD, PUNPCKLWD, and PSRAD are used to accomplish the adaptation but since they all use the MM shifter unit they cannot be paired with each other. Each of the loops were unrolled once so that pairing could be improved. So now in each loop iteration eight coefficients are adapted. The value of m was chosen as a fixed value of 0.125 which is just a shift of three bits to the right. After the new coefficients are generated they must be unpacked into their high and low 16-bit values before they are stored back into memory.
It may be possible to reduce the number of cycles that the echo canceler code performs by making adjustments in how the data arrays are passed into the function to reduce the number of misaligned data accesses. For example, currently the transmit data, txdataI and txdataQ. are passed into the function as sequential arrays and the way the filters operate on them causes misaligned accesses three out four times because the pointer to these arrays is incremented by two bytes for every filter output calculation. Perhaps four copies of the data could be passed in for each the real and imaginary data, each copy being a shifted version of the original array, thus preventing misaligned accesses if the algorithm was thought out with the data in this structure. The overhead of making these multiple copies would be amortized by the fact that the same txdata is used many times as the FIR and adaptation loops execute.
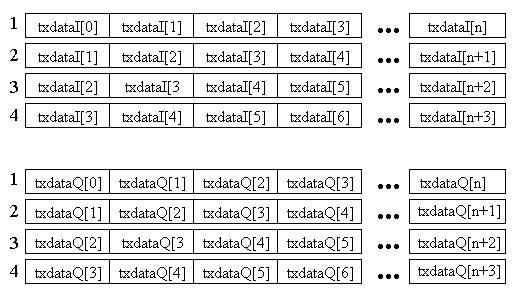
During the calculation of the first filter output, the arrays starting with the txdataI[0] and txdataQ[0] elements would be used. The next filter output would be calculated using the arrays starting with txdataI[1] and txdataQ[1], the next using txdataI[2] and txdataQ[2], and the next using txdataI[3] and txdataQ[3]. The next iteration the pointer to the array could be incremented by 8 bytes and the first arrays could be used for the next calculation.
An even better way, to avoid the problem of having to have eight pointers to the various arrays is to arrange two arrays as described in Figure 8. This way there are only two pointer values that have to be stored and the same amount of memory is used to store the arrays.

;* Description
:
;* This file is an example of one way to implement a baseband echo canceler
;* in MMX technology and will serve as an instructional example.
;*
;* Assumptions:
;*
;* 1. The number of coeffcients in the filters is a multiple of 8.
;* 2. The number of baud being processed is a multiple of four.
;* 3. The arrays passed into this routine are ordered in a specific way
;* described later.
;*
title EchoCancelerMMX
.486P
.model flat, c
; Local Variable Declarations
; 1. Filt_Num - keeps track of which of the three filter is being
; performed
; 2. Baud_Count - number of baud being processed in this block
; 3. Rx_real - address where real received data is stored in memory
; 4. Rx_imag - address where imaginary received data is stored in memory
; 5. dword_mask - word mask used with MMX register
; 6. real_diff1 - used to store the real error signal in this format
; error | 0x0000 | error | 0x0000
; 7. real_diff2 - used to store the real error signal in this format
; 0x0000 | error | 0x0000 | error
; 8. imag_diff1 - used to store the imaginary error signal in this format
; error | 0x0000 | error | 0x0000
; 9. imag_diff2 - used to store the imaginary error signal in this format
; 0x0000 | error | 0x0000 | error
; In the comments for the code the dI array notation indicates the txdataI array
; while the dQ array notation indicates the txdataQ array that are passed in.
; First real set of coefficients start at hIH[0] and go to hIH[n-1] where n is the
; length of the filter and filter #2's coefficients start at hIH[n] and got to
; hIH[2n-1] and filter #3's coefficients start at hIH[2n] and got to hIH[3n-1].
; This is the way hQH array is set up and hIL array and hQL array.
.code
EchoCancelerMMX PROC C uses ebx ecx edx esi edi,
txdataI:PTR WORD,
txdataQ:PTR WORD,
xI:PTR WORD,
xQ:PTR WORD,
hIH:PTR WORD,
hQH:PTR WORD,
hIL:PTR WORD,
hQL:PTR WORD,
h_Leng:DWORD,
x_Leng:DWORD
LOCAL Filt_Num:DWORD
LOCAL Baud_Count:DWORD
LOCAL Rx_real:DWORD
LOCAL Rx_imag:DWORD
LOCAL dword_mask:DWORD
LOCAL real_diff1[2]:DWORD
LOCAL real_diff2[2]:DWORD
LOCAL imag_diff1[2]:DWORD
LOCAL imag_diff2[2]:DWORD
mov Filt_Num, 0000H
mov esi, xI
mov dword_mask, 0FFFFH
mov eax, txdataI
mov ebx, txdataQ
mov Rx_real, esi
mov ecx, hIH
mov esi, xQ
mov edx, hQH
mov Rx_imag, esi
mov esi, x_Leng
mov edi, 0 ; edi = address incrementer for input data
mov Baud_Count, esi
mov esi, h_Leng ; esi = filter length
; This section of code is where the complex FIR is calculated. Before entering
; the loop mm4 is preloaded with first 4 real elements from data array so that
; better pairing can be accomplished. The accumulators mm0 and mm1 are also
; initialized to 0.
FilterLoop:
pxor mm0, mm0
pxor mm1, mm1
sub ecx, edi ; adjust pointer to hIH
sub edx, edi ; adjust pointer to hQH
mov esi, h_Leng ; esi = filter length
pxor mm6, mm6
movq mm4, [eax+edi] ; mm4 = dI[3] | dI[2] | dI[1] | dI[0]
pxor mm5, mm5
mov ebx, txdataQ
movq mm7, mm4
; Complex FIR Loop
FIRLoop:
pmaddwd mm4, [ecx+edi] ; mm4 =
; dI[3]*hIH[3] + dI[2]*hIH[2] |
; dI[1]*hIH[1] + dI[0]*hIH[0]
psubd mm0, mm5 ; mm0 -= mm5 (hQH * dQ)
movq mm5, [ebx+edi] ; mm5 =
; dQ[3] | dQ[2] | dQ[1] | dQ[0]
paddd mm1, mm6 ; mm1 += mm6 (hIH * dQ)
pmaddwd mm7, [edx+edi] ; mm7 =
; dI[3]*hQH[3] + dI[2]*hQH[2] |
; dI[1]*hQH[1] + dI[0]*hQH[0]
movq mm6, mm5 ; mm6 =
; dQ[3] | dQ[2] | dQ[1] | dQ[0]
pmaddwd mm5, [edx+edi] ; mm5 =
; dQ[3]*hQH[3] + dQ[2]*hQH[2] |
; dQ[1]*hQH[1] + dQ[0]*hQH[0]
paddd mm0, mm4 ; mm0 += mm4 (hIH * dI)
movq mm4, [eax+edi+8] ; mm4 =
; dI[3] | dI[2] | dI[1] | dI[0]
pmaddwd mm6, [ecx+edi] ; mm6 =
; dQ[3]*hIH[3] + dQ[2]*hIH[2] |
; dQ[1]*hIH[1] + dQ[0]*hIH[0]
paddd mm1, mm7 ; mm1 += mm7 (hQH * dI)
movq mm7, mm4 ; mm7 =
; dI[3] | dI[2] | dI[1] | dI[0]
add edi, 8 ; increase data pointer by 8 bytes
sub esi, 4 ; decrement counter value
jg FIRLoop ; if >0 then do loop again
;End of Loop for FIR
psubd mm0, mm5 ; mm0 -= mm5 (hQH * dQ)
paddd mm1, mm6 ; mm1 += mm6 (hIH * dQ)
; Here the final complex result of the filter is calculated by copying mm0,
; shifting the copied value 32-bits to the right and adding it back to mm0.
; The same thing is done for the imaginary result in mm1.
; mm0 = yI = (hIH[3,2] * dI[3,2]) - (hQH[3,2] * dQ[3,2])
; | (hIH[1,0] * dI[1,0]) - (hQH[1,0] * dQ[1,0])
; mm1 = yQ = (hIH[3,2] * dQ[3,2]) + (hQH[3,2] * dI[3,2])
; | (hIH[1,0] * dQ[1,0]) + (hQH[1,0] * dI[1,0])
movq mm2, mm0
movq mm3, mm1
movdt mm4, dword_mask
psrlq mm0, 32 ; mm0 = 0x00000000
; | (hIH[3,2]*dI[3,2])-(hQH[3,2]*dQ[3,2])
psrlq mm1, 32 ; mm1 = 0x00000000
; | (hIH[3,2]* Q[3,2])+(hQH[3,2]*dI[3,2])
paddd mm0, mm2 ; mm0 = single real output of filter
; = xxxx | (hIH*dI)-(hQH*dQ)
mov eax, Rx_Real
paddd mm1, mm3 ; mm1 = single imaginary output of filter
; = xxxx | (hIH*dQ)+(hQH*dI)
; This section of code reads in the complex received values and subtracts off the
; filtered value. Then it stores the new received value back into memory and
; stores it back in variables real_diff1, real_diff2, imag_diff1, and imag_diff2
; to be used later in adaptation.
mov ebx, Rx_Imag
psrld mm0, 14 ; adjust output value to lowest 16 bits of mm0
; YI & introduce gain of 2
; xxxx | xxxx | xxxx | YI
movq mm2, [eax]
psrld mm1, 14 ; adjust output value to lowest 16 bits of mm1
; YQ & introduce gain of 2
; xxxx | xxxx | xxxx | YQ
movq mm3, [ebx]
psubw mm2, mm0
psubw mm3, mm1
pand mm2, mm4
pand mm3, mm4
movq mm7, mm2 ; mm7 = 0x0000 | 0x0000 | 0x0000 | xI
movq mm6, mm2 ; mm7 = 0x0000 | 0x0000 | 0x0000 | xI
psllq mm7, 32 ; mm7 = 0x0000 | xI | 0x0000 | 0x0000
movdf ecx, mm2
por mm6, mm7 ; mm6 = 0x0000 | xI | 0x0000 | xI
mov WORD PTR [eax], cx
movq mm7, mm6 ; mm7 = 0x0000 | xI | 0x0000 | xI
add eax, 2
movq mm4, mm3 ; mm5 = 0x0000 | 0x0000 | 0x0000 | xQ
mov Rx_Real, eax
movq mm5, mm3 ; mm5 = 0x0000 | 0x0000 | 0x0000 | xQ
movdf edx, mm3
psllq mm6, 16 ; mm6 = xI | 0x0000 | xI | 0x0000
mov WORD PTR[ebx], dx
add ebx, 2
movq real_diff1, mm6
psllq mm5, 32 ; mm5 = 0x0000 | xQ | 0x0000 | 0x0000
movq real_diff2, mm7
por mm4, mm5 ; mm4 = 0x0000 | xQ | 0x0000 | xQ
mov Rx_Imag, ebx
movq mm5, mm4 ; mm5 = 0x0000 | xQ | 0x0000 | xQ
psllq mm4, 16 ; mm4 = xQ | 0x0000 | xQ | 0x0000
mov ecx, hIH
; Here the base address for the filter coefficients to be adapted is calculated.
; Since the coefficients are stored [hIH0 hIH1 hIH2] and [hIL0 hIL1 hIL2] the
; pointer to the coefficients needs to be adjusted if it is your first iteration
; and hIH0 hIL0 needs to be pointed to, or the second iteration where hIH1 hIL1( =
; (hIH0 hIL0) + 2 * length of filter) needs to be pointed to, or the third
; iteration where hIH2 hIL2( = (hIH0 hIL0) + 4 * length of filter) needs to be
; pointed to.
mov edx, hIL ; load edx with base address of low 16-bits
mov ebx, Filt_Num ; of real filter coefficients
mov eax, h_Leng ; h_Leng = offset needed to point to correct
mov esi, h_Leng ; set of coefficients to be adapted
movq imag_diff1, mm4 ; store imag. error for adaptation
movq imag_diff2, mm5
dec ebx ; determine which filter is being done this
jg real_adapt2 ; time through loop
jl real_adapt
real_adapt1:
shl eax, 1
jmp do_real_adapt
real_adapt2:
shl eax, 2
jmp do_real_adapt
real_adapt:
mov eax, 0
do_real_adapt:
add ecx, eax ; point to correct set of coefficients to
add edx, eax ; adapt
sub edi, esi
mov eax, txdataI
sub edi, esi
mov ebx, txdataQ
sub ecx, edi
sub edx, edi
; This section of code performs the loop that calculates the real coefficient
; adaptation.
; real hnew = real hold + mu * (real error * real data + imag error * imag data)
; mu = 0.125 (shift right by 3 bits)
; real data = txdataI = dI in comments
; real error = xI
; imag data = txdataQ = dQ in comments
; imag error = xQ
; Adaptation loop for real coefficients
Adapt_Real:
movq mm7, real_diff2 ; mm7 = 0x0000 | xI | 0x0000 | xI
movq mm0, mm6 ; mm0 = xI | 0x0000 | xI | 0x0000
pmaddwd mm0, [eax+edi] ; mm0 =xI * dI[3] | xI * dI[1]
movq mm2, mm4 ; mm2 = xQ | 0x0000 | xQ | 0x0000
pmaddwd mm2, [ebx+edi] ; mm2 =xQ * dQ[3] | xQ * dQ[1]
movq mm1, mm7 ; mm1 = 0x0000 | xI | 0x0000 | xI
pmaddwd mm1, [eax+edi] ; mm1 =xI * dI[2] | xI * dI[0]
movq mm3, mm5 ; mm3 = 0x0000 | xQ | 0x0000 | xQ
pmaddwd mm3, [ebx+edi] ; mm3 =xQ * dQ[2] | xQ * dQ[0]
pmaddwd mm6, [eax+edi+8] ; mm6 =xI * dI[7] | xI * dI[5]
paddd mm0, mm2 ; mm0 =xI*dI[3]+xQ*dQ[3] | xI*dI[1]+xQ*dQ[1]
pmaddwd mm4, [ebx+edi+8] ; mm4 =xQ * dQ[7] | xQ * dQ[5]
psrad mm0, 3 ; multiply by mu(0.125)
pmaddwd mm7, [eax+edi+8] ; mm7 =xI * dI[6] | xI * dI[4]
paddd mm1, mm3 ; mm1 = xI*dI[2]+xQ*dQ[2] | xI*dI[0]+xQ*dQ[0]
pmaddwd mm5, [ebx+edi+8] ; mm5 =xQ * dQ[6] | xQ * dQ[4]
psrad mm1, 3 ; multiply by mu(0.125)
movq mm2, mm0 ; mm2 =mu*(xI*dI[3]+xQ*dQ[3] | xI*dI[1]+xQ*dQ[1])
movq mm3, mm1 ; mm3 = mu*(xI*dI[2]+xQ*dQ[2] | xI*dI[0]+xQ*dQ[0])
punpckldq mm1, mm2 ; mm1 = mu*(xI*dI[1]+xQ*dQ[1] | xI*dI[0]+xQ*dQ[0])
paddd mm6, mm4 ; mm6 =xI*dI[7]+xQ*dQ[7] | xI*dI[5]+xQ*dQ[5]
punpckhdq mm3, mm0 ; mm3 = mu*(xI*dI[3]+xQ*dQ[3] | xI*dI[2]+xQ*dQ[2])
paddd mm7, mm5 ; mm7 = xI*dI[6]+xQ*dQ[6] | xI*dI[4]+xQ*dQ[4]
movq mm0, [edx+edi] ; mm0 = hIL[3] | hIL[2] | hIL[1] | hIL[0]
psrad mm6, 3 ; multiply by mu(0.125)
movq mm2, mm0 ; mm2 = hIL[3] | hIL[2] | hIL[1] | hIL[0]
psrad mm7, 3 ; multiply by mu(0.125)
punpckhwd mm0, [ecx+edi] ; mm0 = hIH[3] | hIL[3] | hIH[2] | hIL[2]
movq mm4, mm6 ; mm4 =mu*(xI*dI[7]+xQ*dQ[7] | xI*dI[5]+xQ*dQ[5])
punpcklwd mm2, [ecx+edi] ; mm2 = hIH[1] | hIL[1] | hIH[0] | hIL[0]
movq mm5, mm7 ; mm5 = mu*(xI*dI[6]+xQ*dQ[6] | xI*dI[4]+xQ*dQ[4])
paddd mm0, mm3 ; mm0 = hnew[3,2] = hold[3,2] + mu*error*D
; = hIH[3] | hIL[3] | hIH[2] | hIL[2]
punpckldq mm7, mm4 ; mm7 = mu*(xI*dI[5]+xQ*dQ[5] | xI*dI[4]+xQ*dQ[4])
paddd mm1, mm2 ; mm1 = hnew[1,0] = hold[1,0] + mu*error*D
; = hIH[1] | hIL[1] | hIH[0] | hIL[0]
punpckhdq mm5, mm6 ; mm5 = mu*(xI*dI[7]+xQ*dQ[7] | xI*dI[6]+xQ*dQ[6])
movq mm6, [edx+edi+8] ; mm6 = hIL[7] | hIL[6] | hIL[5] | hIL[4]
movq mm2, mm0 ; mm2 = hnew[3,2] = hold[3,2] + mu*error*D
; = hIH[3] | hIL[3] | hIH[2] | hIL[2]
movq mm4, mm6 ; mm4 = hIL[7] | hIL[6] | hIL[5] | hIL[4]
psrlq mm2, 32 ; mm2 = 0x0000 | 0x0000 | hIH[3] | hIL[3]
punpckhwd mm6, [ecx+edi+8] ; mm6 = hIH[7] | hIL[7] | hIH[6] | hIL[6]
movq mm3, mm1 ; mm3 = hnew[1,0] = hold[1,0] + mu*error*D
; = hIH[1] | hIL[1] | hIH[0] | hIL[0]
punpcklwd mm4, [ecx+edi+8] ; mm4 = hIH[5] | hIL[5] | hIH[4] | hIL[4]
paddd mm6, mm5 ; mm6 = hnew[7,6] = hold[7,6] + mu*error*D
; = hIH[7] | hIL[7] | hIH[6] | hIL[6]
psrlq mm3, 32 ; mm3 = 0x0000 | 0x0000 | hIH[1] | hIL[1]
paddd mm7, mm4 ; mm7 = hnew[5,4] = hold[5,4] + mu*error*D
; = hIH[5] | hIL[5] | hIH[4] | hIL[4]
punpckldq mm2, mm0 ; mm2 = hIH[2] | hIL[2] | hIH[3] | hIL[3]
movq mm4, mm6 ; mm4 = hnew[7,6] = hold[7,6] + mu*error*D
; = hIH[7] | hIL[7] | hIH[6] | hIL[6]
movq mm5, mm7 ; mm5 = hnew[5,4] = hold[5,4] + mu*error*D
punpckldq mm3, mm1 ; mm3 = hIH[0] | hIL[0] | hIH[1] | hIL[1]
punpcklwd mm0, mm2 ; mm0 = hIH[3] | hIH[2] | hIL[3] | hIL[2]
punpcklwd mm1, mm3 ; mm1 = hIH[1] | hIH[0] | hIL[1] | hIL[0]
movq mm3, mm1 ; mm3 = hIH[1] | hIH[0] | hIL[1] | hIL[0]
psrlq mm4, 32 ; mm4 = 0x0000 | 0x0000 | hIH[3] | hIL[3]
psrlq mm5, 32 ; mm5 = 0x0000 | 0x0000 | hIH[5] | hIL[5]
punpckhdq mm3, mm0 ; mm3 = hIH[3] | hIH[2] | hIH[1] | hIH[0]
punpckldq mm1, mm0 ; mm1 = hIL[3] | hIL[2] | hIL[1] | hIL[0]
movq [ecx+edi], mm3 ; store new hIHs back into memory
punpckldq mm4, mm6 ; mm4 = hIH[6] | hIL[6] | hIH[7] | hIL[7]
movq [edx+edi], mm1 ; store new hILs back into memory
punpckldq mm5, mm7 ; mm5 = hIH[4] | hIL[4] | hIH[5] | hIL[5]
punpcklwd mm6, mm4 ; mm6 = hIH[7] | hIH[6] | hIL[7] | hIL[6]
movq mm0, mm5
movq mm4, imag_diff1 ; mm4 = xQ | 0x0000 | xQ | 0x0000
punpcklwd mm7, mm0 ; mm7 = hIH[5] | hIH[4] | hIL[5] | hIL[4]
movq mm0, mm7 ; mm5 = hIH[5] | hIH[4] | hIL[5] | hIL[4]
movq mm1, mm6
movq mm5, imag_diff2 ; mm5 = 0x0000 | xQ | 0x0000 | xQ
punpckldq mm7, mm1 ; mm7 = hIL[7] | hIL[6] | hIL[7] | hIL[6]
movq mm6, real_diff1
punpckhdq mm0, mm1 ; mm5 = hIH[7] | hIH[6] | hIH[5] | hIH[4]
movq [edx+edi+8], mm7 ; store new hILs back into memory
movq [ecx+edi+8], mm0 ; store new hIHs back into memory
add edi, 16
sub esi, 8
jg Adapt_Real
movq mm7, real_diff2 ; mm7 = 0x0000 | xI | 0x0000 | xI
; Here the base address for the imag.filter coefficients to be adapted is calculated.
; Since the coefficients are stored [hQH0 hQH1 hQH2] and [hQL0 hQL1 hQL2] the
; pointer to the coefficients needs to be adjusted if it is your first iteration
; and hQH0 hQL0 needs to be pointed to, or the second iteration where hQH1 hQL1( =
; (hQH0 hQL0) + 2 * length of filter) needs to be pointed to, or the third
; iteration where hQH2 hQL2( = (hQH0 hQL0) + 4 * length of filter) needs to be
; pointed to.
mov ecx, hQH
mov edx, hQL ; load edx with base address of low 16-bits
; of imaginary filter coefficients
mov ebx, Filt_Num ; h_Leng = offset needed to point to correct
mov eax, h_Leng ; set of coefficients to be adapted
mov esi, h_Leng
dec ebx
jg imag_adapt2
jl imag_adapt
imag_adapt1:
shl eax, 1
jmp do_imag_adapt
imag_adapt2:
shl eax, 2
jmp do_imag_adapt
imag_adapt:
mov eax, 0
do_imag_adapt:
add ecx, eax ; point to correct set of coefficients to
add edx, eax ; adapt
sub edi, esi
mov eax, txdataI
sub edi, esi
mov ebx, txdataQ
sub ecx, edi
sub edx, edi
; This section of code performs the loop that calculates the imag. coefficient
; adaptation.
; imag hnew = imag hold + mu * (imag error * real data - real error * imag data)
; mu = 0.125 (shift right by 3 bits)
; real data = txdataI = dI in comments
; real error = xI
; imag data = txdataQ = dQ in comments
; imag error = xQ
; Adaptation loop for imaginary coefficients
Adapt_Imag:
movq mm4, imag_diff2 ; mm7 = xQ | 0x0000 | xQ | 0x0000
movq mm3, mm5 ; mm3 = 0x0000 | xQ | 0x0000 | xQ
pmaddwd mm3, [eax+edi] ; mm3 =xQ * dI[2] | xQ * dI[0]
movq mm1, mm7 ; mm1 = 0x0000 | xI | 0x0000 | xI
pmaddwd mm1, [ebx+edi] ; mm1 =xI * dQ[2] | xI * dQ[0]
movq mm0, mm6 ; mm0 = xI | 0x0000 | xI | 0x0000
pmaddwd mm0, [ebx+edi] ; mm0 =xI * dQ[3] | xI * dQ[1]
movq mm2, mm4 ; mm2 = xQ | 0x0000 | xQ | 0x0000
pmaddwd mm2, [eax+edi] ; mm2 =xQ * dI[3] | xQ * dI[1]
pmaddwd mm6, [ebx+edi+8] ; mm6 =xI * dQ[7] | xI * dQ[5]
psubd mm3, mm1 ; mm3 = xQ*dI[2]-xI*dQ[2] | xQ*dI[0]-xI*dQ[0]
pmaddwd mm4, [eax+edi+8] ; mm4 =xQ * dI[7] | xQ * dI[5]
psrad mm3, 3 ; multiply by mu(0.125)
pmaddwd mm7, [ebx+edi+8] ; mm7 =xI * dQ[6] | xI * dQ[4]
psubd mm2, mm0 ; mm2 =xQ*dI[3]-xI*dQ[3] | xQ*dI[1]-xI*dQ[1]
pmaddwd mm5, [eax+edi+8] ; mm5 =xQ * dI[6] | xQ * dI[4]
psrad mm2, 3 ; multiply by mu(0.125)
movq mm0, mm2 ; mm0 =mu*(xQ*dI[3]-xI*dQ[3] | xQ*dI[1]-xI*dQ[1])
movq mm1, mm3 ; mm1 = mu*(xQ*dI[2]-xI*dQ[2] | xQ*dI[0]-xI*dQ[0])
punpckldq mm1, mm2 ; mm1 = mu*(xQ*dI[1]-xI*dQ[1] | xQ*dI[0]-xI*dQ[0])
psubd mm4, mm6 ; mm4 =xQ*dI[7]-xI*dQ[7] | xQ*dI[5]-xI*dQ[5]
punpckhdq mm3, mm0 ; mm3 = mu*(xQ*dI[3]-xI*dQ[3] | xQ*dI[2]-xI*dQ[2])
psubd mm5, mm7 ; mm5 = xQ*dI[6]-xI*dQ[6] | xQ*dI[4]-xI*dQ[4]
movq mm0, [edx+edi] ; mm0 = hQL[3] | hQL[2] | hQL[1] | hQL[0]
psrad mm4, 3 ; multiply by mu(0.125)
movq mm2, mm0 ; mm2 = hQL[3] | hQL[2] | hQL[1] | hQL[0]
psrad mm5, 3 ; multiply by mu(0.125)
punpckhwd mm0, [ecx+edi] ; mm0 = hQH[3] | hQL[3] | hQH[2] | hQL[2]
movq mm6, mm4 ; mm6 =mu*(xQ*dI[7]-xI*dQ[7] | xQ*dI[5]-xI*dQ[5])
punpcklwd mm2, [ecx+edi] ; mm2 = hQH[1] | hQL[1] | hQH[0] | hQL[0]
movq mm7, mm5 ; mm7 = mu*(xQ*dI[6]-xI*dQ[6] | xQ*dI[4]-xI*dQ[4])
paddd mm0, mm3 ; mm0 = hnew[3,2] = hold[3,2] + mu*error*D
; = hQH[3] | hQL[3] | hQH[2] | hQL[2]
punpckldq mm7, mm4 ; mm7 = mu*(xQ*dI[5]-xI*dQ[5] | xQ*dI[4]-xI*dQ[4])
paddd mm2, mm1 ; mm2 = hnew[1,0] = hold[1,0] + mu*error*D
; = hQH[1] | hQL[1] | hQH[0] | hQL[0]
punpckhdq mm5, mm6 ; mm5 = mu*(xQ*dI[7]-xI*dQ[7] | xQ*dI[6]-xI*dQ[6])
movq mm6, [edx+edi+8] ; mm6 = hQL[7] | hQL[6] | hQL[5] | hQL[4]
movq mm1, mm0 ; mm1 = hnew[3,2] = hold[3,2] + mu*error*D
; = hQH[3] | hQL[3] | hQH[2] | hQL[2]
movq mm4, mm6 ; mm4 = hQL[7] | hQL[6] | hQL[5] | hQL[4]
psrlq mm1, 32 ; mm1 = 0x0000 | 0x0000 | hQH[3] | hQL[3]
punpckhwd mm6, [ecx+edi+8] ; mm6 = hQH[7] | hQL[7] | hQH[6] | hQL[6]
movq mm3, mm2 ; mm3 = hnew[1,0] = hold[1,0] + mu*error*D
; = hQH[1] | hQL[1] | hQH[0] | hQL[0]
punpcklwd mm4, [ecx+edi+8] ; mm4 = hQH[5] | hQL[5] | hQH[4] | hQL[4]
paddd mm6, mm5 ; mm6 = hnew[7,6] = hold[7,6] + mu*error*D
; = hQH[7] | hQL[7] | hQH[6] | hQL[6]
psrlq mm3, 32 ; mm3 = 0X0000 | 0X0000 | hQH[1] | hQL[1]
paddd mm4, mm7 ; mm4 = hnew[1,0] = hold[1,0] + mu*error*D
; = hQH[1] | hQL[1] | hQH[0] | hQL[0]
punpckldq mm1, mm0 ; mm1 = hQH[2] | hQL[2] | hQH[3] | hQL[3]
movq mm7, mm6 ; mm7 = hnew[7,6] = hold[7,6] + mu*error*D
; = hQH[7] | hQL[7] | hQH[6] | hQL[6]
movq mm5, mm4 ; mm5 = hnew[5,4] = hold[5,4] + mu*error*D
; = hQH[5] | hQL[5] | hQH[4] | hQL[4]
punpckldq mm3, mm2 ; mm3 = hQH[0] | hQL[0] | hQH[1] | hQL[1]
punpcklwd mm0, mm1 ; mm0 = hQH[3] | hQH[2] | hQL[3] | hQL[2]
punpcklwd mm2, mm3 ; mm2 = hQH[1] | hQH[0] | hQL[1] | hQL[0]
movq mm3, mm2 ; mm3 = hQH[1] | hQH[0] | hQL[1] | hQL[0]
psrlq mm7, 32 ; mm7 = 0x0000 | 0x0000 | hQH[7] | hQL[7]
psrlq mm5, 32 ; mm5 = 0X0000 | 0X0000 | hQH[5] | hQL[5]
punpckhdq mm2, mm0 ; mm2 = hQH[3] | hQH[2] | hQH[1] | hQH[0]
punpckldq mm3, mm0 ; mm3 = hQL[3] | hQL[2] | hQL[1] | hQL[0]
movq [ecx+edi], mm2 ; store new hQHs back into memory
punpckldq mm7, mm6 ; mm7 = hQH[6] | hQL[6] | hQH[7] | hQL[7]
movq [edx+edi], mm3 ; store new hQLs back into memory
punpckldq mm5, mm4 ; mm5 = hQH[4] | hQL[4] | hQH[5] | hQL[5]
punpcklwd mm6, mm7 ; mm6 = hQH[7] | hQH[6] | hQL[7] | hQL[6]
movq mm0, mm5
movq mm5, imag_diff2 ; mm5 = 0x0000 | xI | 0x0000 | xI
punpcklwd mm4, mm0 ; mm4 = hQH[5] | hQH[4] | hQL[5] | hQL[4]
movq mm0, mm4 ; mm5 = hQH[5] | hQH[4] | hQL[5] | hQL[4]
movq mm1, mm6
movq mm6, real_diff1 ; mm6 = xQ | 0x0000 | xQ | 0x0000
punpckldq mm0, mm1 ; mm5 = hQL[7] | hQL[6] | hQL[5] | hQL[4]
movq mm7, real_diff2 ; mm7 = 0x0000 | xQ | 0x0000 | xQ
punpckhdq mm4, mm1 ; mm4 = hQH[7] | hQH[6] | hQH[5] | hQH[4]
movq [edx+edi+8], mm0 ; store new hQLs back into memory
movq [ecx+edi+8], mm4 ; store new hQHs back into memory
add edi, 16
sub esi, 8
jg Adapt_Imag
; This section of code determines which of the three filters is to be done next
mov esi, h_Leng
mov ecx, hIH
mov edx, hQH
sub edi, esi
mov ebx, Filt_Num
sub edi, esi
dec ebx
je filter2
jg filter0
filter1: ; iteration = 1
mov esi, h_Leng ; esi = h_Leng
inc ebx
shl esi, 1 ; esi = 2*hLeng
inc ebx ; Filt_Num = 1
mov Filt_Num, ebx ; Filt_Num = 1 for next time
add ecx, esi ; ecx = hIH + 2*h_Leng
add edx, esi ; edx = hQH + 2*h_Leng
jmp FilterLoop
filter2: ; iteration = 2
mov esi, h_Leng ; esi = h_Leng
inc ebx
shl esi, 2 ; esi = 4*hLeng
inc ebx ; Filt_Num = 2
mov Filt_Num, ebx ; Filt_Num = 2 for next time
add ecx, esi ; ecx = hIH + 4*h_Leng
add edx, esi ; edx = hQH + 4*h_Leng
jmp FilterLoop
filter0: ; iteration = 0
dec ebx ; Filt_Num = 0
mov esi, Baud_Count
mov Filt_Num, ebx ; Filt_Num = 0 for next time
add edi, 2
; Check to see if block of baud has been processed. If so then ecmmx is done!
; If not continue computation.
dec esi
mov Baud_Count, esi
jne FilterLoop
emms ; empty floating point stack
ret
EchoCancelerMMX EndP
END